CF #247. K-мод

к-мод гэж дараах нөхцлүүдийг хангах модыг нэрлэе:
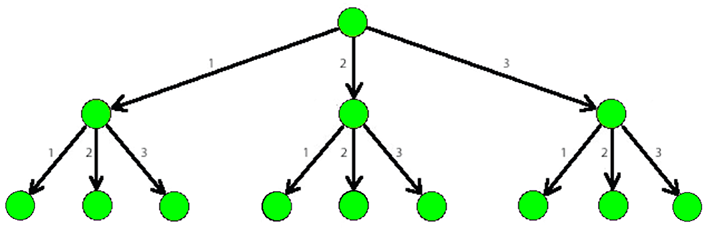
- орой бүр к ширхэг хүүтэй байна
- ирмэг бүр тодорхой жинтэй байна
- орой бүрийн хувьд хүү оройтой нь холбосон ирмэгүүд 1, ..., к гэсэн жингүүдтэй байна
Доорх зурагт 3-модны хэсгийг үзүүлэв:

Дараах асуултын хариуг ол:
"к-модны үндэснээс эхэлсэн, дайрч өнгөрөх ирмэгүүдийн нийт жин нь n-тэй тэнцүү байх, d-гээс багагүй жинтэй ядаж нэг ирмэг агуулах замын тоо хэд байх вэ?"
Энэ тоо нь маш том байж болох тул түүнийг 1000000007 (10^9+7) тоонд хуваасны үлдэгдлийг олоорой.

Оролт
Ганц мөрөнд n, k болон d (1 ≤ n, k ≤ 100; 1 ≤ d ≤ k) тонууд өгөгдөнө.

Гаралт
Бодлогын хариуг 1000000007 (10^9+7) тоонд хуваасны үлдэгдлийг хэвлэнэ.